策略的核心是背后的交易思想，数学模型只是交易思想的数量化表达，如果交易思想错了，那再复杂高深的数学也于事无补。

由于经营量化社群的原因，能看到的量化圈子稍微比萌新们大一些，我真的看过很多量化大神的实盘策略，涉及到的数学都没有超过高中范畴，但策略成功的原因并不完全在数学本身，而在于宽客将数学理论与交易实际相结合的能力，也就是要把“数学”用到刀刃上。

道理大家都懂（无论高深还是浅显），关键是要学以致用。抛砖引玉，就拿之前量化大神的两个策略出来溜溜，它们的共同点就是都涉及到一个基础的数学概念，高中就学习过的，那就是“导数”，看看大神是怎么把“导数”玩出花儿来。

策略1：日内波动极值策略

第一个要介绍的策略就是『日内波动极值策略』，它起源于广发金工在11年前发布的研报《基于日内波动极值的股指期货趋势跟随系统》，最初是用在股指期货的量化交易上。

对于交易者而言，有波动才有价差（无论是向上还是向下），有价差才有低买高卖，才有投资收益。正如原文中所言，投机人只有溶于波动的市场中才有机会博取高额收益，平静无奇的市场只能是一潭死水，若市场波动很小，更极端一点，在一条近乎直线走势的市场中，无论何种策略、无论采用何种模型，都是无法赚钱的，神仙亦乏术。

那我们如何拥抱波动，抓取波段呢？其中一个方法就是利用日内波动极值的思想实现趋势跟随。

随着市场的单边趋势运行，价格波动极值会逐步被突破，而这种突破又是上下两个方向均可的。如果价格向上突破极值点，那么我们认为随后的价格波动继续向上的可能是偏大的，同理如果价格向下突破极值点，那么我们认为随后的价格波动继续向下的可能会偏大，从而形成趋势跟随策略。价格起伏就像波浪，后面的价格突破了前浪的高点，很可能孕育着一次比前浪更汹涌的后浪。

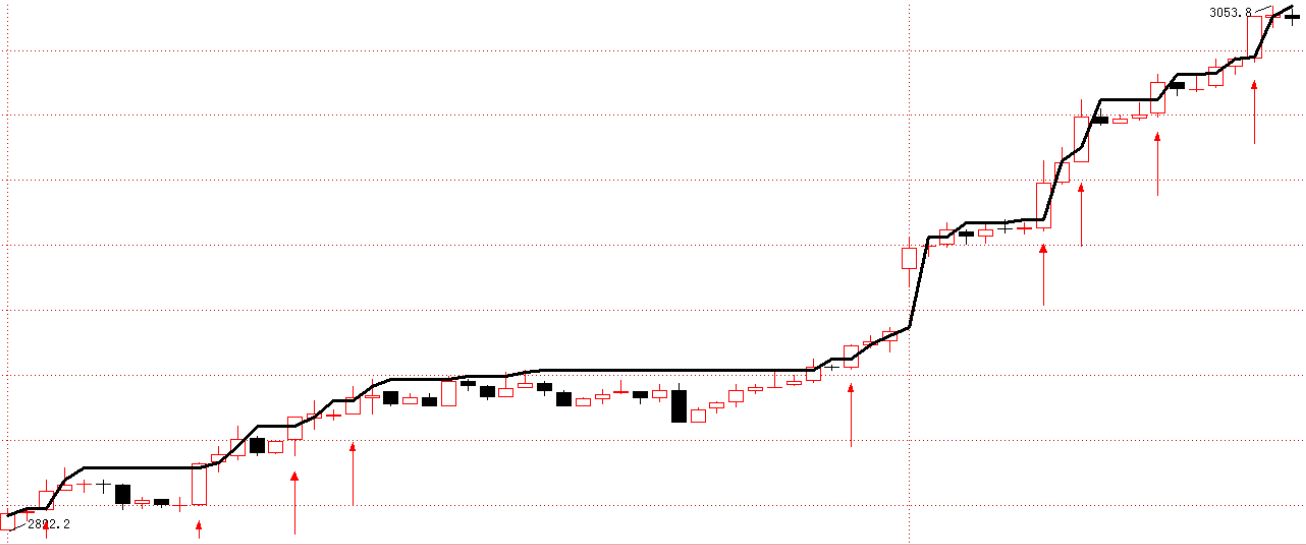接着来定义和计算价格波动极值，原文中是基于日内行情的价格进行计算，具体来讲，日内某个时点的极值，就是自当日开盘以来截止至当前时点，市场创出的最高值或者最低值，前者称为日内极高值，后者称为日内极低值。

这就形成了一个很朴素的量化策略，首先选取某一信号观察频率周期（如5分钟K线），当价格向上穿越日内波动极高值时发出买入信号，当价格向下穿越极低值时发出卖出信号，关于“日内极值计算细节”、“开仓后如何来跟踪持有的头寸”、“何时平仓离场的问题”、“回测费率设置”等方面，请详见研报原文。研报发布时披露的回测交易资金曲线如下所示。

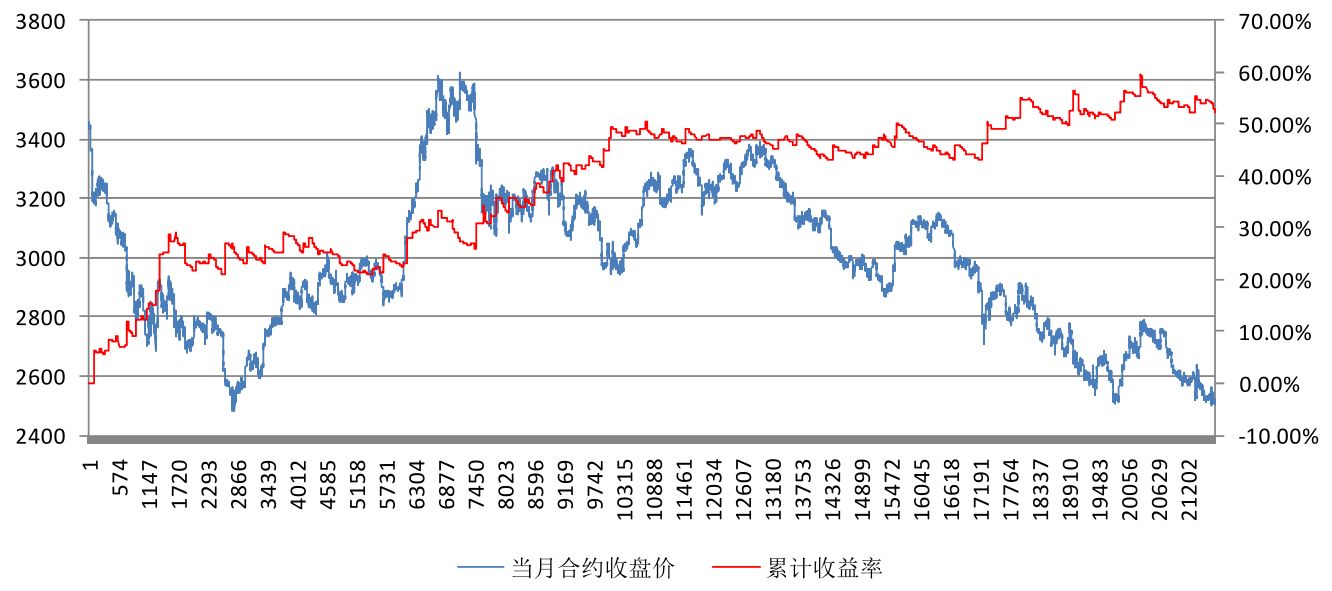当时这个日内波动极值策略只是应用在了股指期货品种上，后来被某私募量化大神发现该策略的挖掘潜力，觉得极值的确定还可以利用高中数学课学过的“导数”，将改进后的策略分别移植到了商品期货和股票上，并有偿地进行了小范围的分享。

众所周知，若一元函数可导，则在极大值或极小值处，导数为0。使用求导的方式确定波动极值，进而衡量K线的形态和走势，还是利用之前的策略的大体思想进行策略构建，不过细节上有所变化。

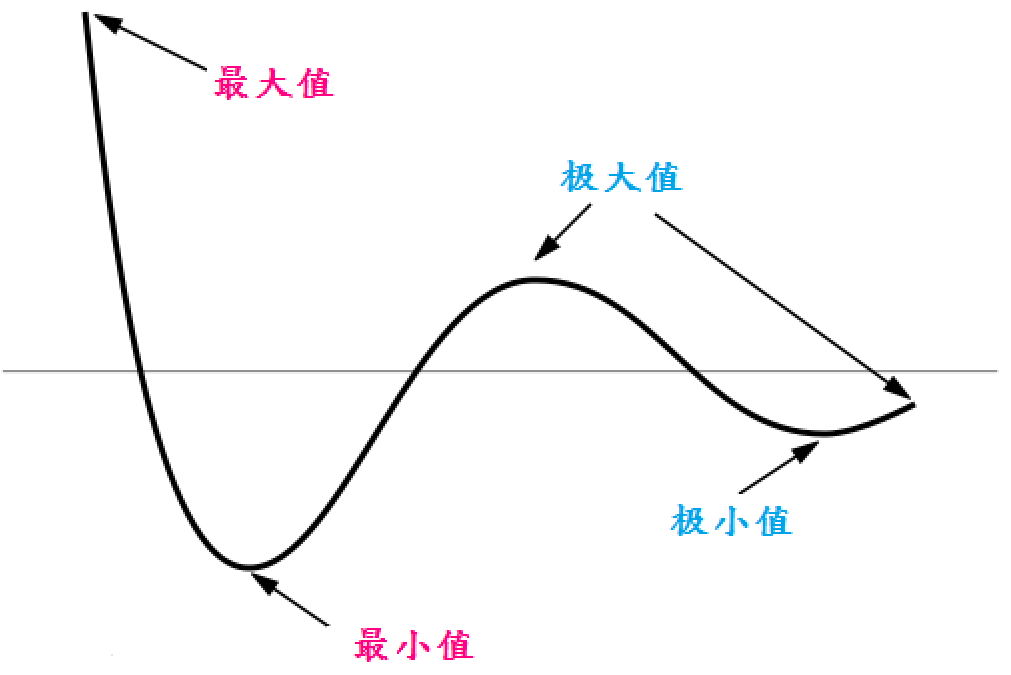
百度百科中关于“极值求导”的说明：函数在其整个定义域内可能有许多极大值或极小值，而且某个极大值不一定大于某个极小值。函数的极值通过其一阶和二阶导数来确定。对于一元可微函数f(x)，它在某点x0有极值的充分必要条件是f(x)在x0的某邻域上一阶可导，在x0处二阶可导，且f'(X0)=0，f"(x0)≠0，那么：
1）若f"（x0）<0，则f在x0取得极大值；
2）若f"（x0）>0，则f在x0取得极小值。

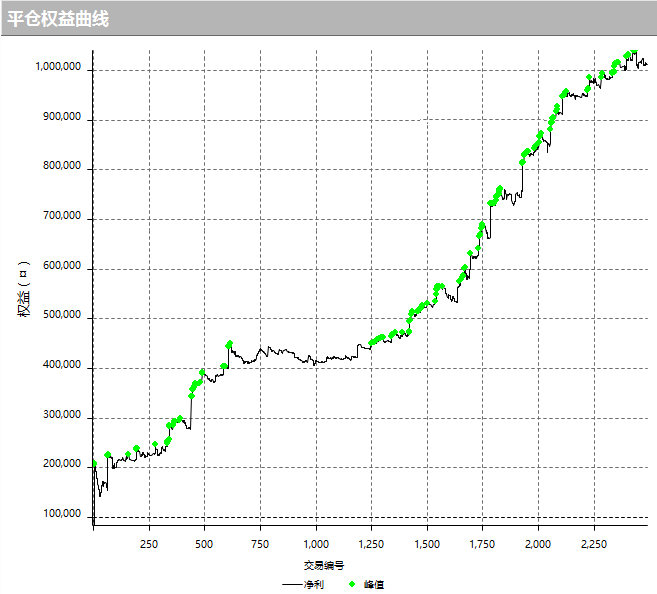
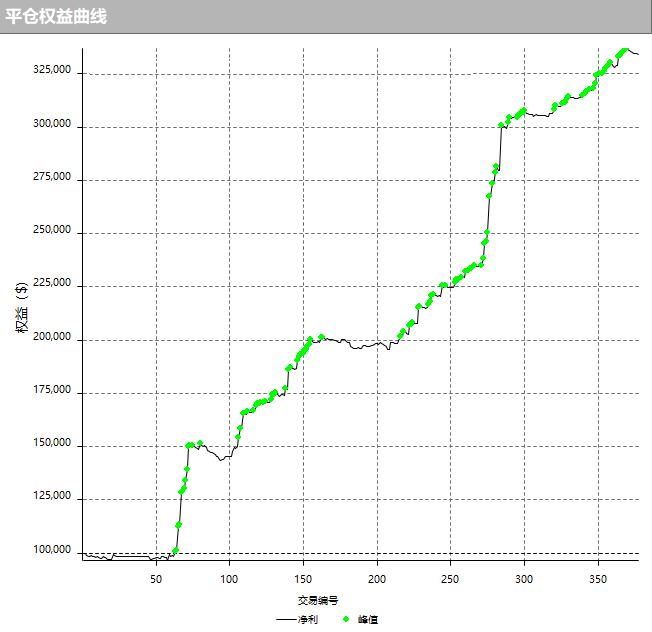
私募量化大神改进后的商品期货策略盈亏曲线：

私募量化大神改进后的股票策略盈亏曲线：

策略2：基于低阶多项式拟合的日内趋势策略

这第二个策略就是『基于低阶多项式拟合的日内趋势策略』，这个日内策略与第一个策略师出同门，它的策略思想出自于广发金工的另外一篇研报《基于低阶多项式拟合的股指期货趋势交易(LPTT)策略》

传统金融理论认为在高效率市场中，股票、期货等金融产品的价格变化服从马尔科夫随机过程，即具有无记忆特征，也就谈不上价格变动的趋势。但是在市场效率不高的情况下，由于信息流动存在不平衡性，股票或期货的价格变动常常会形成单边趋势，此时若能够顺势交易，则有可能获得有效的趋势价差收益。

那如何捕捉这个价格趋势呢？该研报中的交易策略采用的理论基础是离散数据的多项式拟合。

别被这么专业的名词唬住了，其实啊，只要高中数学课认真上过，我一说你就明白了。

研报标题中提到的“低阶多项式拟合”，其实指的就是一阶多项式拟合和二阶多项式拟合，一阶多项式拟合指的就是把离散的价格序列拟合成线性函数y1=a·x+b，二阶多项式拟合就是拟合成二次函数y2=a·x^2+b·x+c。看吧，高中数学课上都学过吧~

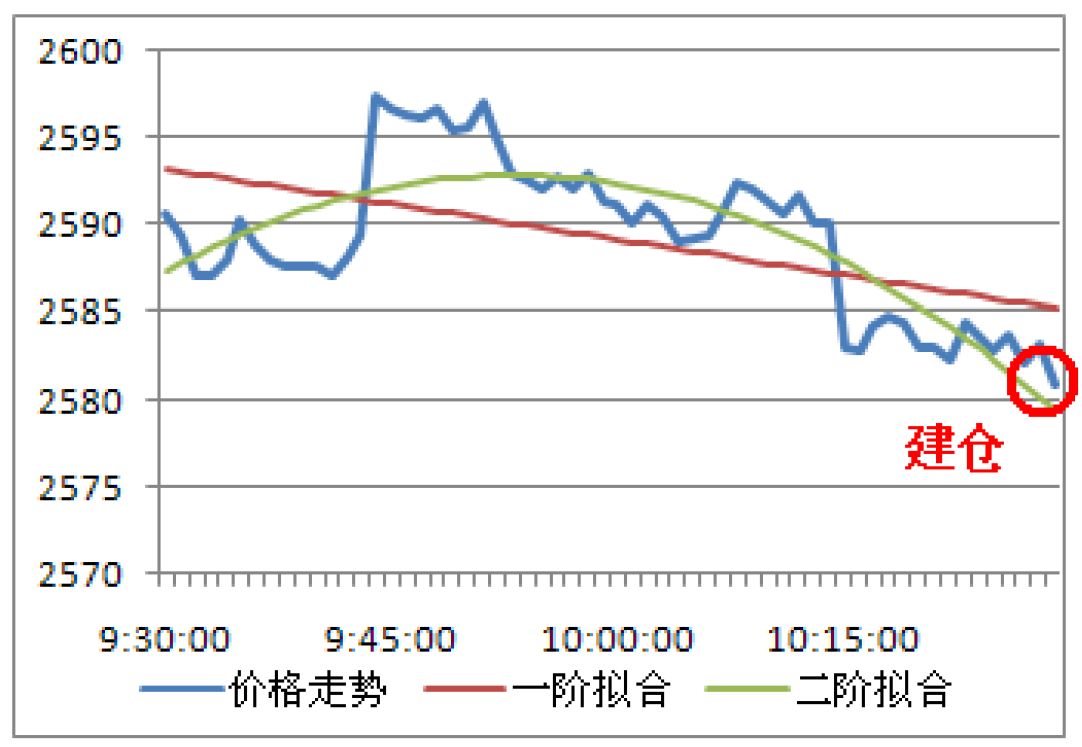若对一阶线性函数求一阶导数，也就是平常所说的斜率，若导数dy/dt>0，说明价格正处于上升趋势；若导数dy/dt<0，则为下跌趋势。

若对二阶线性函数求二阶导数，若二阶导数d2y/dt2>0，价格曲线为凹（开口向上）；若二阶导数d2y/dt2<0，价格曲线为凸（开口向下）。

做个类比，价格曲线就像汽车行走的距离轨迹，对距离（位移）求一阶导数就是速度，速度大于0说明朝正方向开，小于0说明朝反方向开。求二阶导数就是加速度，假设此时汽车为正向行驶，加速度大于0说明在汽车速度还在增加的状态当中，在不断加速，反之则是处在减速的过程当中。

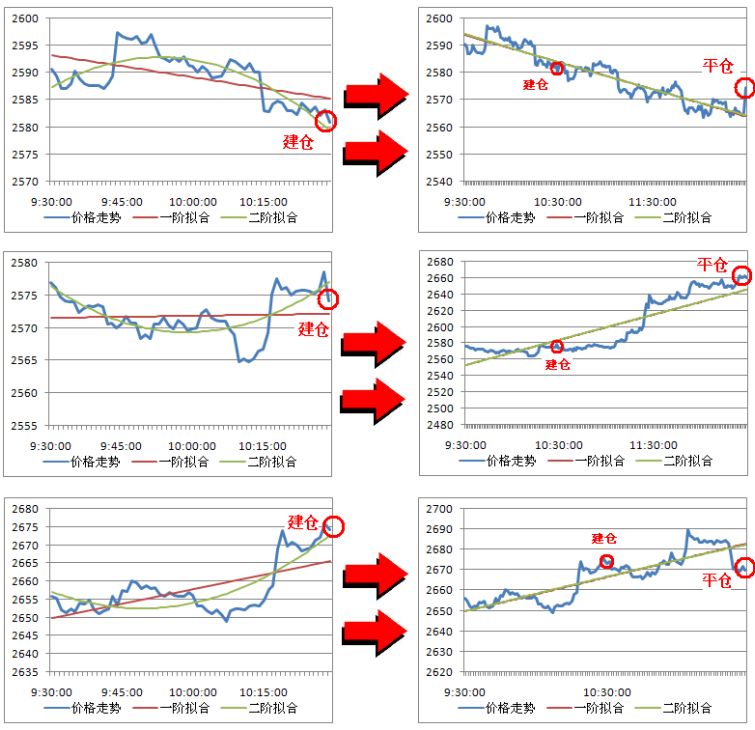
因此，结合线性函数的一阶导数和二次函数的二阶导数，可以把价格序列划分为如下四种状态。

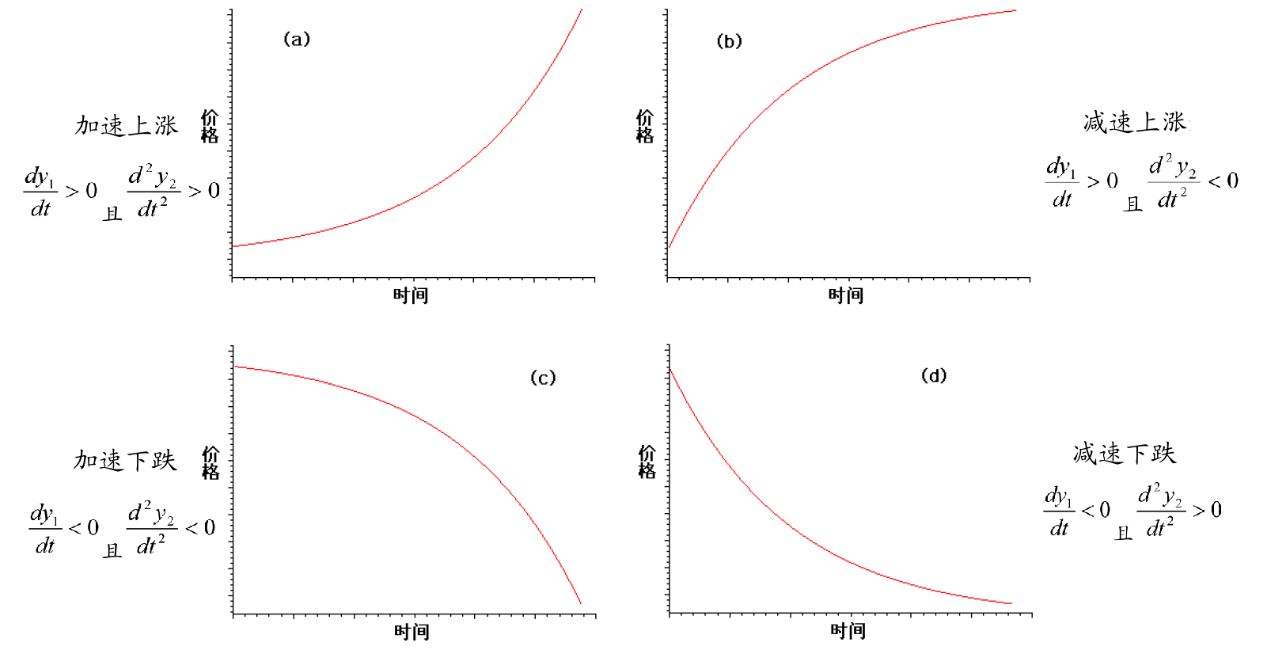朴素的策略思想这就跟着来了，*假设线性函数的一阶导数和二次函数的二阶导数分别为g1和g2，当g1g2>0时，说明出现了加速上涨或加速下跌的情况，便可以根据价格方向顺势开仓。**

当g1正负号发生改变时，说明价格趋势改变，该种情况需要进行平仓。

当g2正负号发生改变时，说明于上涨或下跌趋势由加速变为减速，趋势有结束迹象，该种情况也需要进行平仓。

还有就是在尾盘进行强制平仓，日内策略不持仓过夜。

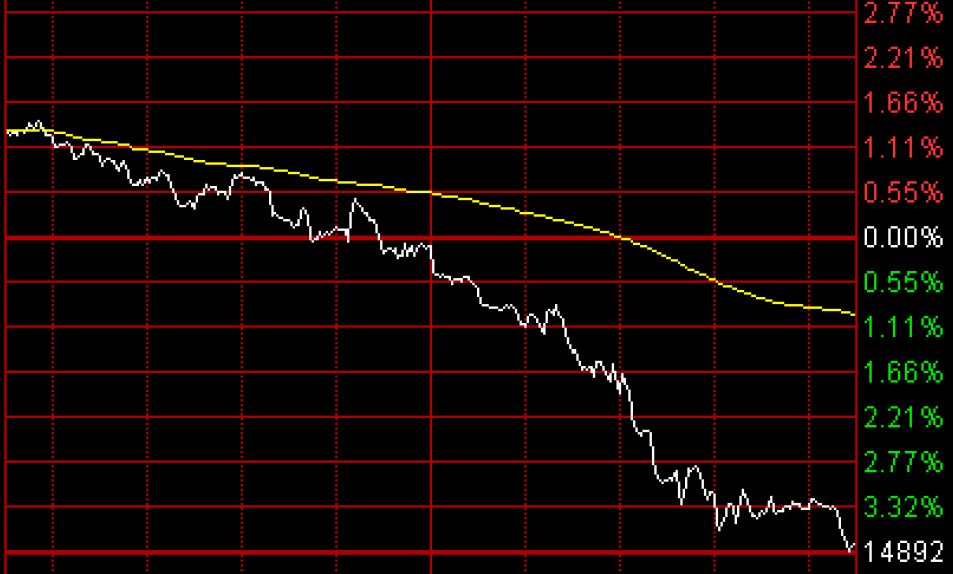
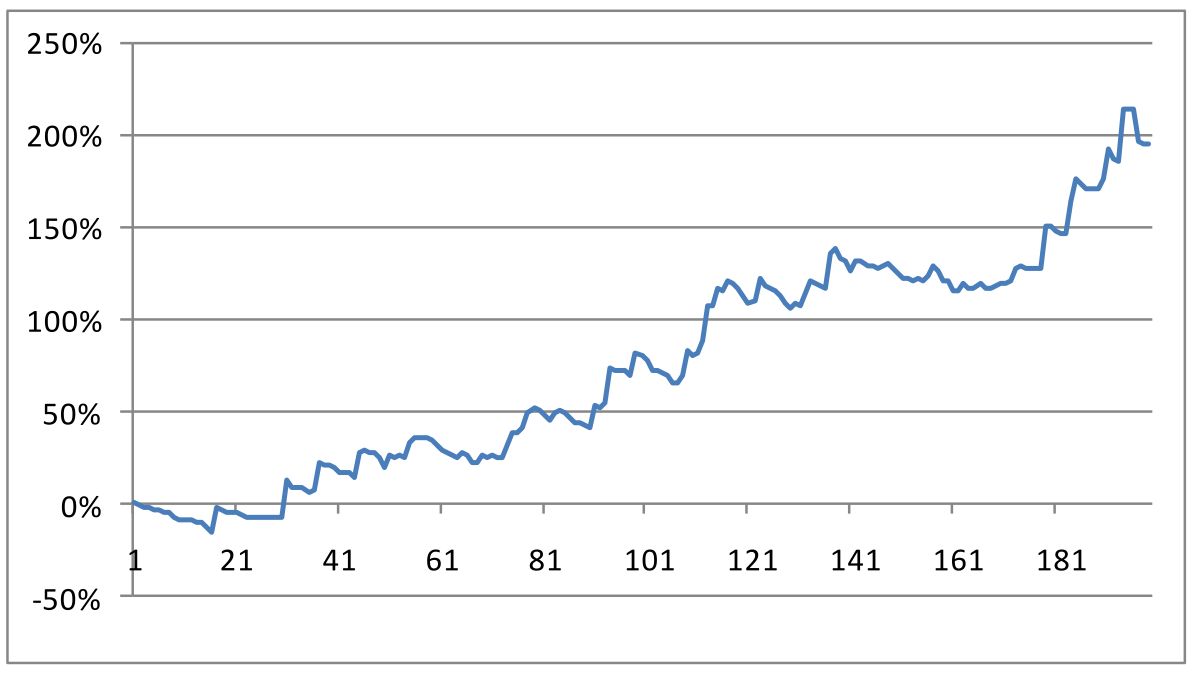
在研报当中，交易标的是股指期货，回测的累计收益率曲线如下所示。

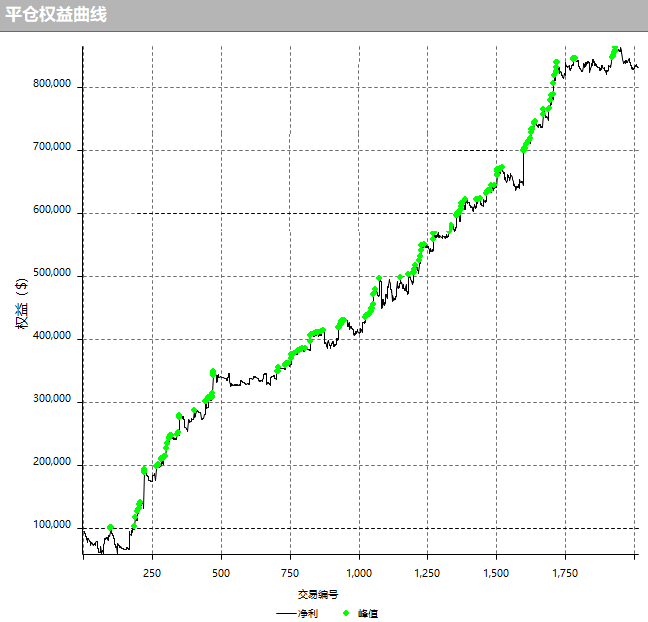
还是这位私募量化大神，将其研报中的策略精髓移植到商品期货和股票之上，实现了交易开拓者TB、文华财经、金字塔、MultiCharts和TradeStation多个版本的源码，移植到商品期货多品种上的回测累计收益率曲线如下所示。

总结一下

从上面介绍的两个量化策略看出，核心思路就是要抓到大价差和大波段，第一个策略关键是找到极值点，第二个策略关键是做一、二阶拟合，看上去手段形式不一样，实质上都可以用“导数”来解决。

“导数”只是高中数学当中的一个基础概念，不算高深，但策略能成功，靠的是宽客对数学概念学以致用的能力，以上两个策略例子只是给大伙儿做个启发，起到抛砖引玉的作用。据我路边社小道不靠谱消息透露，类似于“导数”用于量化策略的数学概念还有：偏度、峰度、协方差......

最后补充说明一下，本文不是说“高深的数学”就不需要了，而是鼓励萌新们从自身知识水平出发，日拱一卒，小步快进，把学习曲线从陡峭降为平坦，不再焦虑。

Be quant，have fun！